The flight computer, a pilot's essential tool!

The flight computer, better known by its name E-6B, is a slide rule designed for aeronautical use. It was developed in the late ’30s by Lieutenant Philip Dalton to simplify calculations for pilots. The first versions were made of fluorescent plastic, but are now available in aluminum or cardboard. The flight computer is made up of two discs, one fixed and the other rotating. Let’s find out how it works!

How does it work?

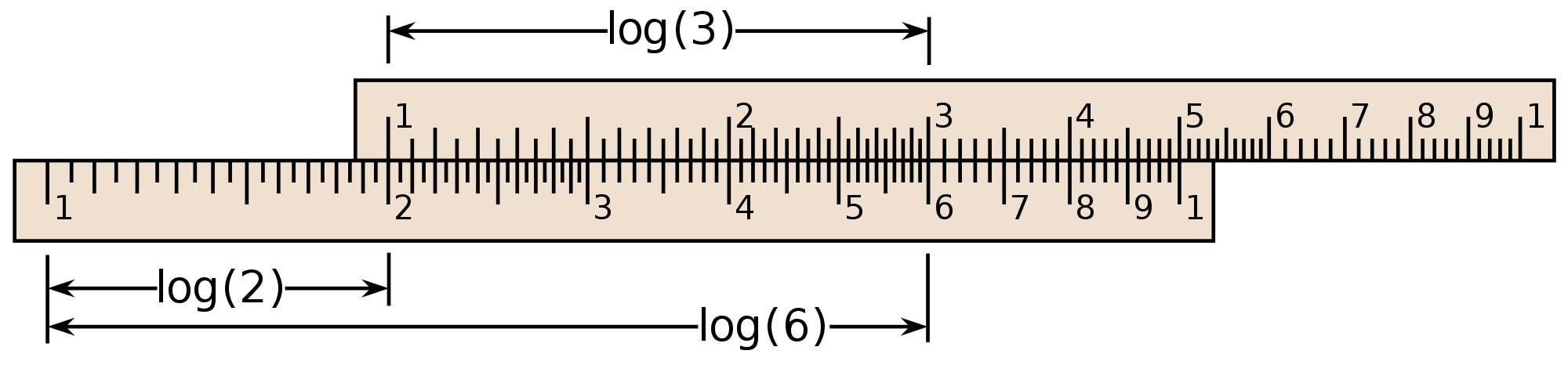
Each disc is graduated on a logarithmic scale. This makes it possible to perform multiplications, thanks to the following property: log(a*b) = log(a) + log(b). It can also be explained as follows: multiplying a and b corresponds to adding the logarithmic length of a and b. So there’s nothing magical about it, just mathematics!

Description

The computer has two main faces: the first is a circular slide rule and the second is a wind and ground speed correction calculator.

The slide rule has 3 scales. The outer scale (in black) is fixed, while the other two (in grey) are printed on a rotating disk. The innermost scale is graduated in hours, while the other two are graduated on the same logarithmic scale.

The wind calculator lets you solve trigonometric problems graphically. It features a transparent window over a rotating disk graduated in degrees. A sliding part with several speed arcs completes it.

Having completed the presentation, it’s time to move on to the main calculations that a flight computer can offer.

Multiplication

Let’s start with the basics: multiplication! Let’s take a simple example like 3 times 4. We place the number 30 under the index 10. Then, under the 40 of the outer scale, we read the answer: 12.

Note: We’ve just created a correspondence table between the two discs. This means that for a number N on the outer disc, we’ll get the result N x 3 on the lower disc. We can see from this example that the number 30 represents the number 3. It can also represent 300, 3000, 30,000… or 0.3, 0.03, 0.003…

It is therefore necessary to estimate the order of magnitude of the result.

Division

To divide, simply place the divisor under the number to be divided. The answer is above index 10 on the outer scale.

The same applies to the interpretation of quantities as for multiplication.

Rapport

Let’s say we flew 38 nautical miles in 25 minutes. How fast are we flying? Simply rotate the inner disc to match the number 25 below the number 38 (bottom red arrow). We read the speed above index 60, i.e. around 91 knots (top red arrow).

The flight computer lets you calculate your ground speed in the flick of a wrist ( or disc!).

Calcul de temps et de consommation

Our plane has a cruising speed of 120 knots and a fuel consumption of 35 liters per hour. We need to reach an airport 190 nautical miles away. How long and how much fuel do we need to reach the airport?

We place index 60 of the lower disc under 12 of the outer disc. Search for 19, or 190 miles, on the outer disc. The answer in minutes is just below, 95 minutes. You can also convert minutes into hours by looking at the hour scale, here 1 h 35.

To find out how much fuel you need, place index 60 on the lower disc under 35 on the outer disc. The answer is above 95, or about 55.5 liters.

Calcul de dérive

This time we use the reverse side of the computer, after selecting the “High speed” or “Low speed” side on the sliding part. We’re going to calculate the drift with a 280° wind at 20 knots.

Rotate the transparent disk until the wind direction is displayed under the “True index” (here 280°). Starting from the center of the disk, place a point representing the wind speed. To do this, we use the central axis where, for this computer, each graduation is worth 2 knots.

We then place our heading (here 030°) under the “True index” and our “wind” point on the arc corresponding to our air speed (here 120 knots).

The center of the disk indicates our ground speed, approximately 127 knots. The drift corresponds to the difference between the center line and the wind point, i.e. 9°. These 9° must be subtracted from our heading, as we’re on the left, so we need to take a heading of 021°.

I’ve just shown you the main functions of a flight computer, but there are many more that I won’t go into here. For example, it is possible to calculate the time to reach a VOR station, calculate density altitude, TAS, Mach number…

To find out more about this subject, I recommend the book “Le computer eXpliqué au pilote privé” published by Cépaduès, which comes with a cardboard computer to assemble.